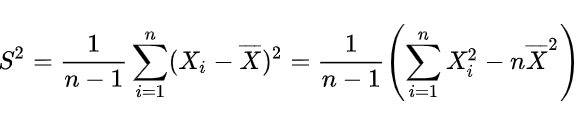
样本方差的公式为  其中x拔 为样本均值. 样本均值=（1+2+3+4+5）/5=3 s^2=(（1-3）^2+(2-3)^2+(3-3)^2+(4-3)^2+(5-3)^2)/4=2.5

要计算样本方差，我们首先需要找到样本的均值，然后计算每个样本点与均值之间差的平方，最后求这些平方差的平均值。

### 计算步骤：

1. **计算样本均值**：
\[
\text{均值} = \frac{1 + 2 + 3 + 4 + 5}{5} = \frac{15}{5} = 3
\]

2. **计算每个数据点与均值的差的平方**：
\[
(1-3)^2 = (-2)^2 = 4
\]
\[
(2-3)^2 = (-1)^2 = 1
\]
\[
(3-3)^2 = 0^2 = 0
\]
\[
(4-3)^2 = 1^2 = 1
\]
\[
(5-3)^2 = 2^2 = 4
\]

3. **求这些平方差的和并计算平均值**：
\[
\text{平方差的和} = 4 + 1 + 0 + 1 + 4 = 10
\]
\[
\text{样本方差} = \frac{10}{5} = 2
\]

在选项中，并没有 2 这个数值，样本方差的计算有一点点误解，我们需要注意的是样本方差的计算公式和总体方差的区别，样本方差通常采用无偏估计即：
\[
\text{样本方差(s}^2\text{)} = \frac{\sum (x_i - \bar{x})^2}{n - 1}
\]
计算如下：
\[
\text{样本方差} = \frac{10}{5 - 1} = \frac{10}{4} = 2.5
\]

因此，正确答案是 **B: 2.5**。