以下哪个语句可以输出如图 3-110 所示的内容？ 

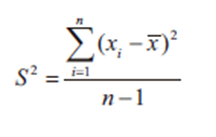
要计算样本数据的方差，我们可以按照以下步骤进行：

1. **计算样本均值（平均值）**：
样本数据为 \(1, 3, 5, 7, 9\)，样本量 \(n = 5\)。

样本均值 \(\bar{x}\) 计算公式为：
\[
\bar{x} = \frac{1 + 3 + 5 + 7 + 9}{5} = \frac{25}{5} = 5
\]

2. **计算每个数据点与均值的差的平方**：
\[
(1 - 5)^2 = (-4)^2 = 16
\]
\[
(3 - 5)^2 = (-2)^2 = 4
\]
\[
(5 - 5)^2 = 0^2 = 0
\]
\[
(7 - 5)^2 = 2^2 = 4
\]
\[
(9 - 5)^2 = 4^2 = 16
\]

3. **计算这些平方差的总和**：
\[
16 + 4 + 0 + 4 + 16 = 40
\]

4. **计算样本方差**：
样本方差的公式为：
\[
s^2 = \frac{\sum (x_i - \bar{x})^2}{n - 1}
\]
其中 \(n - 1\) 是自由度。

代入数据：
\[
s^2 = \frac{40}{5 - 1} = \frac{40}{4} = 10
\]

因此，这组样本数据的方差为 10。正确答案是 B: 10。