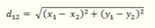
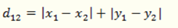
欧式距离：  曼哈顿距离：  汉明距离： 两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数 杰卡德距离： 

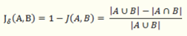
正确答案是：B: 曼哈顿距离

**专业分析：**

1. **欧氏距离（Euclidean Distance）**：
欧氏距离是指在欧几里得空间中两个点之间的直线距离，计算公式为：
\[
d = \sqrt{\sum_{i=1}^{n} (x_i - y_i)^2}
\]
其中，\( x_i \) 和 \( y_i \) 分别是两个点在第 \( i \) 个维度上的坐标。

2. **曼哈顿距离（Manhattan Distance）**：
曼哈顿距离也称为城市街区距离或L1距离，是指在标准坐标系上，两个点在各个维度上的绝对轴距总和，计算公式为：
\[
d = \sum_{i=1}^{n} |x_i - y_i|
\]
其中，\( x_i \) 和 \( y_i \) 分别是两个点在第 \( i \) 个维度上的坐标。

3. **汉明距离（Hamming Distance）**：
汉明距离用于计算两个等长字符串之间的不同字符的个数，常用于信息编码领域，公式为：
\[
d = \sum_{i=1}^{n} (x_i \neq y_i)
\]
其中，\( x_i \) 和 \( y_i \) 分别是两个字符串在第 \( i \) 个位置上的字符。

4. **杰卡德距离（Jaccard Distance）**：
杰卡德距离用于衡量两个集合的相似性和差异性，计算公式为：
\[
d = 1 - \frac{|A \cap B|}{|A \cup B|}
\]
其中，\( A \) 和 \( B \) 是两个集合，\( |A \cap B| \) 是两个集合的交集的大小，\( |A \cup B| \) 是两个集合的并集的大小。

综上所述，两个点在标准坐标系上的绝对轴距总和指的是曼哈顿距离。因此，正确答案是B: 曼哈顿距离。