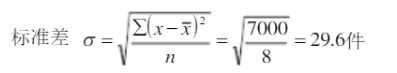
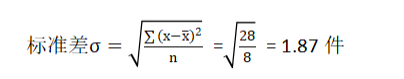
要计算总体标准差，我们需要先计算每个班组的平均产量，然后计算每个工人产量与平均产量的差值的平方和，最后取平方根。

首先计算甲班组的平均产量：
\[ \bar{X}_{甲} = \frac{20 + 40 + 60 + 70 + 80 + 100 + 120 + 70}{8} = \frac{560}{8} = 70 \]

然后计算乙班组的平均产量：
\[ \bar{X}_{乙} = \frac{67 + 68 + 69 + 70 + 71 + 72 + 73 + 70}{8} = \frac{560}{8} = 70 \]

接下来计算甲班组的方差：
\[ S^2_{\甲} = \frac{(20-70)^2 + (40-70)^2 + (60-70)^2 + (70-70)^2 + (80-70)^2 + (100-70)^2 + (120-70)^2 + (70-70)^2}{8} \]
\[ = \frac{2500 + 900 + 100 + 0 + 100 + 900 + 2500 + 0}{8} = \frac{7000}{8} = 875 \]

甲班组的标准差：
\[ S_{\甲} = \sqrt{875} \approx 29.6 \]

接下来计算乙班组的方差：
\[ S^2_{\乙} = \frac{(67-70)^2 + (68-70)^2 + (69-70)^2 + (70-70)^2 + (71-70)^2 + (72-70)^2 + (73-70)^2 + (70-70)^2}{8} \]
\[ = \frac{9 + 4 + 1 + 0 + 1 + 4 + 9 + 0}{8} = \frac{28}{8} = 3.5 \]

乙班组的标准差：
\[ S_{\乙} = \sqrt{3.5} \approx 1.87 \]

因此，正确答案是：
\[ C: 甲班组29.6，乙班组1.87 \]